Matrix regresi linear. Persamaan garis linear.

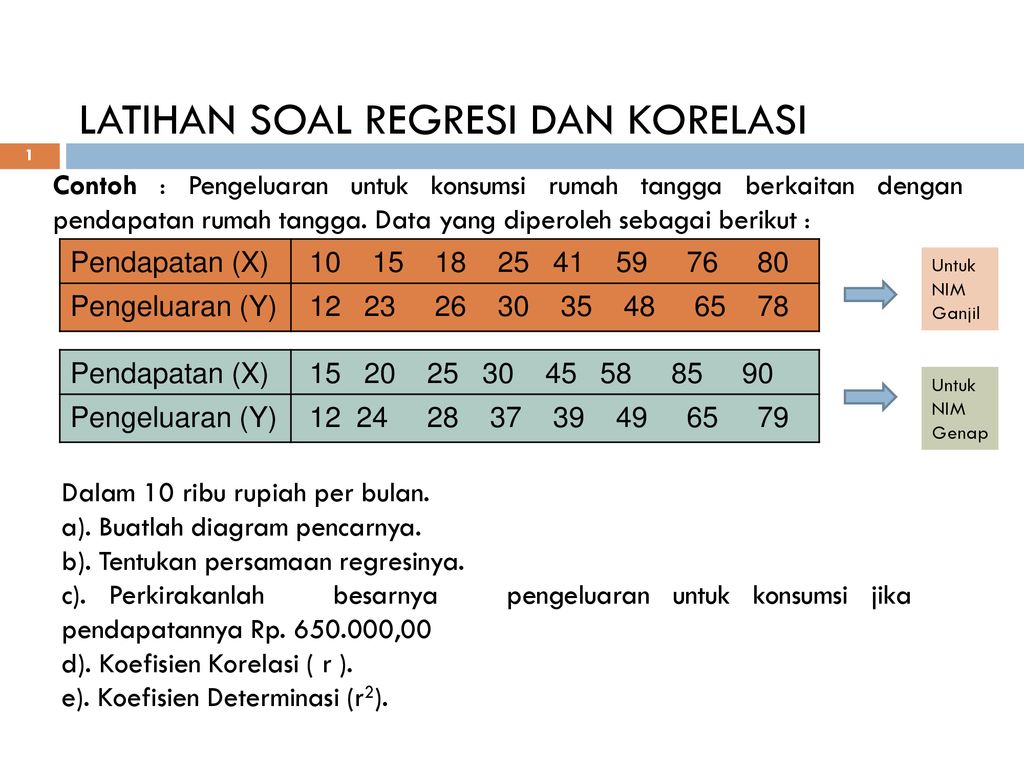
Contoh Analisis Regresi Sederhana
Contoh soal persamaan regresi. Terdapat tiga jenis regresi yang digunakan sesuai dengan tujuan analisis yaitu regresi linier sederhana regresi linier berganda dan regresi non linear. Analisis regresi linear sederhana regresi linear sederhana adalah metode statistik yang berfungsi untuk menguji sejauh mana hubungan sebab akibat antara variabel faktor penyebab x terhadap variabel akibatnyafaktor penyebab pada umumnya dilambangkan dengan x atau disebut juga dengan predictor sedangkan variabel akibat dilambangkan dengan y atau disebut juga dengan response. Sebagai contoh misalnya titik a 13 dan titik b 9 maka persamaan garis linear yang dapat dibuat adalah. Y 936 27 x b. Academiaedu is a platform for academics to share research papers. Jadi a1 dan b2 sehingga persamaannya y1 2x.
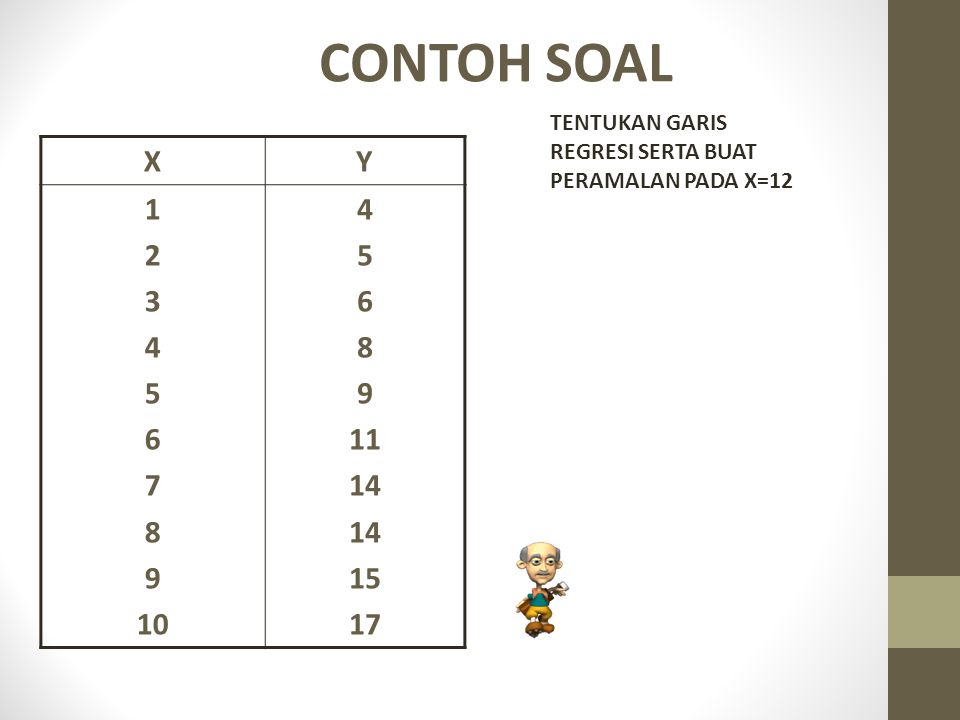
Y a b x maka persamaan regresi dalam soal ini adalah. Maka persamaan regresi dalam soal ini adalah. Contoh penggunaan analisis regresi linear sederhana dalam produksi antara lain. Analisis regresi adalah studi tentang masalah hubungan beberapa variabel yang ditampilkan dalam persamaan matematika andi 2009. Dalam bentuk matrik bisa kita buat persaman sebagai berikut. Menentukan persamaan regresi linier sederhana.
Contoh soal regresi linier berganda dalam suatu penelitian yang dilakukan terhadap 10 rumah tangga yang diilih secara acak diperoleh data pengeluaran untuk pembelian barang barang tahan lama per minggu y pendapatan per minggu x 1 dan jumlah anggota rumah tangga x 2 sebagai berikut. Menentukan besarnya koefisien korelasi dan koefisien determinasi. Diketahui suatu penelitian terhadap hubungan antara nilai biaya periklanan dengan tingkat penjualan dari sebuah koperasi adalah sebagai berikut. Selanjutnya langkah langkah dalam pengambilan data sama halnya dalam uji 2 variabel bebas yaitu dilanjutkan dengan mencari nilai r dengan menggunakan persamaan sebagai berikut. Uji signifikansi persamaan garis regresi tersebut dengan langkah langkah pada uji signifikansi dalam 2 variabel bebas hanya saja tambahkan persamaan berikut pada uji signifikansi 3 variabel bebas. Jadi persamaan regresi gandanya y 1282 052 x 1 017 x 2 untuk membandingkan f hitung dengan f tabel sebelumnya akan dicari nilai korelasi ganda dengan taraf signifikan.
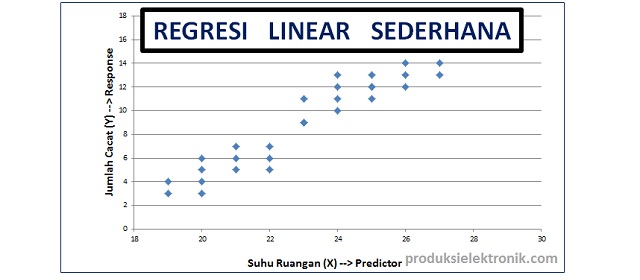
Y 936 27 x b. R n xy x. Analisis regresi lebih akurat dalam melakukan analisis korelasi peramalan atau perkiraan nilai variabel terikat pada nilai variabel bebas lebih akurat pula karena pada analisis ini kesulitan dalam menunjukkan slop tingkat perubahan suatu variabel terhadap. Regresi linier sederhana regresi digunakan untuk melihat bentuk hubungan antar variabel melalui suatu persamaan.